Lower bounds for sorting
worst case에서 nlgn보다 빠른 comparison sort(원소의 순서를 정할 때 비교만 사용하는 정렬)가 없다.
참고) heap sort랑 merge sort가 worst case에서 O(nlgn)
The decision-tree model
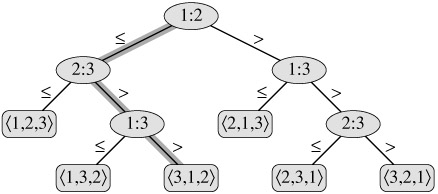
출처 : http://serverbob.3x.ro/IA/DDU0048.html
모든 원소가 구별되는 값(distinct)이라면
input의 모든 원소를 ai <= aj 로 표현할 수 있다.
comparison sort를 decision trees로 볼 수 있다.
내부 노드 (i,j)는 ai<=aj 임을 의미한다.
각각의 잎노드는 input 원소의 순열(permutation)이다.
decision tree의 루트부터 leaf까지의 path는 sorting algorithm의 수행하고 같다.
가장 긴 path의 길이는 worst case를 의미한다.
즉, worst case는 트리의 높이와 같다.
모든 comparison sort algorithm은 worst case일 때 Ω(nlgn) 만큼 비교한다.
n! <= 2^h (n!은 총 잎의 갯수, h는 트리의 높이)
h>= lg(n!)
h = Ω(nlgn) ( 왜냐하면 lg(n!) = Θ(nlgn) )
Counting sort
n개의 입력원소가 정수이고 범위가 0부터 k(k<=n)일 때라고 가정한다.
"입력원소 x는 x보다 작은 원소의 수가 i-1개 라면 정렬후에는 i에 위치해야 한다." 라는 원리
집합 A의 원소의 범위가 0~k일 때, 집합 A의 원소의 값이 집합 C의 i와 같으면 Ci값에 1을 추가한다. 집합 C는 A의 원소의 범위가 0~k이므로 k+1크기의 배열이면 된다. C는 A원소의 횟수를 저장한 집합이 된다. C'는 C의 누적합이다. (C'[i] = C[0] + ... + C[i])
이 C'를 이용해서 A를 정렬을 할 수 있다. C'i의 값이 a라고 하면 이는 i보다 작거나 같은 값이 집합 A에 a개 있다는 소리다. 그래서 i가 들어갈 자리는 a가 될수 있다.
Stable(입력값이 같은 값이 있을 때 그 순서를 결과값에도 유지 시키는 것)하게 하기 위해서 A의 맨 끝에 있는 원소부터 C'를 이용해서 위치를 찾는다.
수행시간
Θ(n+k)
Θ(k) : C를 0으로 초기화
Θ(n) : A를 스캔하면서 C에 카운터를 증가.
Θ(k) : C를 스캔해서 C' 구하기
Θ(n) : C'과 A를 이용해서 정렬된 집합 B를 구하기. B[C'[A[j]] <- A[j]
k가 O(n)이면 수행시간은 Θ(n)!
Radix sort
n 자리수 숫자들이 있을 때 각 자리수끼리 정렬.
1) 최대유효숫자 -> 최소유효숫자
최대유효숫자부터 정렬. 이전 그룹을 유지하면서 정렬을 해줘야 바르게 정렬이 된다.
2) 최소유효숫자 -> 최대유효숫자
최소유효숫자부터 정렬.
정렬할 때 stable한 sort 알고리즘을 쓴다.
각 자리수의 범위가 k일 때 d 자리인 n개의 수를 radix sort한 수행시간은?
k가 안크면 counting sort 사용하면 된다.
Θ(d(n+k)) (n+k을 d번한거)
d가 상수고, k = O(n)일 때 radix sort는 linear한 소트이다.
b-bit인 수 n개를, r<=b일 때, r개씩 자르고 radix-sort로 정렬했을 때 수행시간은?
Θ((b/r)(n+2^r)) time.
b/r은 d이고 2^r은 k.
예를 들면
32bit를 8bit씩 4개로 나눠서 4자리씩 radix sort.
r=8, b=32, k는 8bit로 0부터 2^8-1까지, 0부터 255까지 표현할 수 있으니 256개 필요하고, b/r=4, n+2^r = n+256.
Θ((b/r)(n+2^r))을 최소화하는 r
1. b < floor(lgn) 일 때
r<=b 이므로 (n+2^r)은 Θ(n)
그래서 r=b일때, (b/b)(n+2^b) = Θ(n)
2. b >= floor(lg n) 일 때
r=floor(lg n)을 선택는 것이 최적이다. (b/lgn)(n+2^(lgn) = (b/lgn)(2n) = Θ(bn/lg n)
r이 floor(lg n)보다 커지면 2^r은 기하급수적으로 증가하고
r이 floor(lg n)보다 작아지면 b/r은 커지고 n+2^r 은 Θ(n)이 된다.
따라서 1,2 종합해보면 r=lg n씩 자를 때가 최적이다.
Radix sort가 퀵소트보다 좋을까?
Radix sort는 Θ(n)이고 퀵소트는 Θ(nlgn) 이니 radix sort가 더 좋을 것 같다.
퀵소트보다 각단계(pass)의 횟수가 작을 수가 있지만 Θ(n)에 감춰진 상수값이 클 수가 있다. 즉, Radix sort의 각각의 pass에서 오래 걸릴 수 있다. 그리고 퀵소트는 하드웨어 캐쉬를 더 효과적으로 사용해서 더 빨리 처리된다. 그리고 Radix는 sort in place가 아니다. 정렬하면서 중간값을 저장할 공간이 더 필요하다. 이런점에서 메모리가 좋다면, in-place 알고리즘인 퀵소트가 빠르다.
퀵소트와 캐쉬 locality를 설명한 글 참고
http://soyoja.tistory.com/248#comment1449755
worst case에서 nlgn보다 빠른 comparison sort(원소의 순서를 정할 때 비교만 사용하는 정렬)가 없다.
참고) heap sort랑 merge sort가 worst case에서 O(nlgn)
The decision-tree model

출처 : http://serverbob.3x.ro/IA/DDU0048.html
모든 원소가 구별되는 값(distinct)이라면
input의 모든 원소를 ai <= aj 로 표현할 수 있다.
comparison sort를 decision trees로 볼 수 있다.
내부 노드 (i,j)는 ai<=aj 임을 의미한다.
각각의 잎노드는 input 원소의 순열(permutation)이다.
decision tree의 루트부터 leaf까지의 path는 sorting algorithm의 수행하고 같다.
가장 긴 path의 길이는 worst case를 의미한다.
즉, worst case는 트리의 높이와 같다.
모든 comparison sort algorithm은 worst case일 때 Ω(nlgn) 만큼 비교한다.
n! <= 2^h (n!은 총 잎의 갯수, h는 트리의 높이)
h>= lg(n!)
h = Ω(nlgn) ( 왜냐하면 lg(n!) = Θ(nlgn) )
Counting sort
n개의 입력원소가 정수이고 범위가 0부터 k(k<=n)일 때라고 가정한다.
"입력원소 x는 x보다 작은 원소의 수가 i-1개 라면 정렬후에는 i에 위치해야 한다." 라는 원리
집합 A의 원소의 범위가 0~k일 때, 집합 A의 원소의 값이 집합 C의 i와 같으면 Ci값에 1을 추가한다. 집합 C는 A의 원소의 범위가 0~k이므로 k+1크기의 배열이면 된다. C는 A원소의 횟수를 저장한 집합이 된다. C'는 C의 누적합이다. (C'[i] = C[0] + ... + C[i])
이 C'를 이용해서 A를 정렬을 할 수 있다. C'i의 값이 a라고 하면 이는 i보다 작거나 같은 값이 집합 A에 a개 있다는 소리다. 그래서 i가 들어갈 자리는 a가 될수 있다.
Stable(입력값이 같은 값이 있을 때 그 순서를 결과값에도 유지 시키는 것)하게 하기 위해서 A의 맨 끝에 있는 원소부터 C'를 이용해서 위치를 찾는다.
수행시간
Θ(n+k)
Θ(k) : C를 0으로 초기화
Θ(n) : A를 스캔하면서 C에 카운터를 증가.
Θ(k) : C를 스캔해서 C' 구하기
Θ(n) : C'과 A를 이용해서 정렬된 집합 B를 구하기. B[C'[A[j]] <- A[j]
k가 O(n)이면 수행시간은 Θ(n)!
Radix sort
n 자리수 숫자들이 있을 때 각 자리수끼리 정렬.
1) 최대유효숫자 -> 최소유효숫자
최대유효숫자부터 정렬. 이전 그룹을 유지하면서 정렬을 해줘야 바르게 정렬이 된다.
2) 최소유효숫자 -> 최대유효숫자
최소유효숫자부터 정렬.
정렬할 때 stable한 sort 알고리즘을 쓴다.
각 자리수의 범위가 k일 때 d 자리인 n개의 수를 radix sort한 수행시간은?
k가 안크면 counting sort 사용하면 된다.
Θ(d(n+k)) (n+k을 d번한거)
d가 상수고, k = O(n)일 때 radix sort는 linear한 소트이다.
b-bit인 수 n개를, r<=b일 때, r개씩 자르고 radix-sort로 정렬했을 때 수행시간은?
Θ((b/r)(n+2^r)) time.
b/r은 d이고 2^r은 k.
예를 들면
32bit를 8bit씩 4개로 나눠서 4자리씩 radix sort.
r=8, b=32, k는 8bit로 0부터 2^8-1까지, 0부터 255까지 표현할 수 있으니 256개 필요하고, b/r=4, n+2^r = n+256.
Θ((b/r)(n+2^r))을 최소화하는 r
1. b < floor(lgn) 일 때
r<=b 이므로 (n+2^r)은 Θ(n)
그래서 r=b일때, (b/b)(n+2^b) = Θ(n)
2. b >= floor(lg n) 일 때
r=floor(lg n)을 선택는 것이 최적이다. (b/lgn)(n+2^(lgn) = (b/lgn)(2n) = Θ(bn/lg n)
r이 floor(lg n)보다 커지면 2^r은 기하급수적으로 증가하고
r이 floor(lg n)보다 작아지면 b/r은 커지고 n+2^r 은 Θ(n)이 된다.
따라서 1,2 종합해보면 r=lg n씩 자를 때가 최적이다.
Radix sort가 퀵소트보다 좋을까?
Radix sort는 Θ(n)이고 퀵소트는 Θ(nlgn) 이니 radix sort가 더 좋을 것 같다.
퀵소트보다 각단계(pass)의 횟수가 작을 수가 있지만 Θ(n)에 감춰진 상수값이 클 수가 있다. 즉, Radix sort의 각각의 pass에서 오래 걸릴 수 있다. 그리고 퀵소트는 하드웨어 캐쉬를 더 효과적으로 사용해서 더 빨리 처리된다. 그리고 Radix는 sort in place가 아니다. 정렬하면서 중간값을 저장할 공간이 더 필요하다. 이런점에서 메모리가 좋다면, in-place 알고리즘인 퀵소트가 빠르다.
퀵소트와 캐쉬 locality를 설명한 글 참고
http://soyoja.tistory.com/248#comment1449755
'공부 > 알고리즘' 카테고리의 다른 글
| Dynamic Programming (0) | 2011.07.09 |
|---|---|
| 11장 Hash Table (0) | 2011.07.08 |
| 7장 Quicksort (0) | 2011.07.03 |
| Heapsort (1) | 2011.06.30 |
| 4 Recursion (0) | 2011.06.28 |
