skyjump's blog

Block matrix multiplication

A block partitioned matrix product can be formed involving operations only on the submatrices. Given an 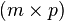 matrix  with q row partitions and s column partitions

and a  matrix  with s row partitions and r column partitions

the matrix product

can be formed blockwise, yielding 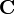 as an  matrix with q row partitions and r column partitions. The matrices in your matrix 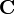 are calculated by multiplying while you multiply:

 
Inverse = non singular
No Inverse = singular
즉, 역행렬을 가지면 정상이고 못가지면 이상한거란다. 무슨 기준이지?ㅋㅋ
아무튼 역행렬을 못가지는 행렬이 있다.
어떨때 못가질까? 첫번째는 고딩때 배웠던 determinant를 이용하는 것. 2x2일 때 ad-bc = 0 이면 역행렬이 없다.
두번째는 A 가 (a11, a12, a21, a22)가 (1,3,2,6)이라고 하자. determinant로는 0이 나오므로 역행렬을 못가진다. 진짜 그럴까?
얘가 역행렬을 가진다고 치자. 그러면 Ax = I 인 x가 있을 것이다. 자, column 벡터를 생각해보자. (1,3)이랑 (2,6) 벡터로 (1,0)이나 (0,1)을 표현할 수 있나? 없다. 따라서 A는 역행렬이 없다. column 벡터를 보면 역행렬을 왜 가질 수 없는지 알 수 있다.
마지막 세번째는 Ax = 0 에서 0이 아닌 vector x가 있으면 A는 역행렬을 못가진다. 이유는 뭘까? A의 역행렬을 가진다고 쳐보자. 그럼 Ax = 0 에서 양변에 A^-1 해주면 x = 0이다. 0이 아닌 벡터 x가 있다고 했는데 0이 나와버렸으니 모순이다.

The Gauss-Jordan Method
역행렬을 구하는 방법이다.
가우스 조단 방법을 모른다고 하고 2x2 역행렬을 구한다고 하면
AA^-1 = I 여기서 A^-1을 (a,b,c,d)로 놓고 A에서 A^-1의 각 컬럼을 곱하면 
식이 두개가 나온다. 하나는 결과가 (1,0) ,나머지는 (0,1)인 행렬식 두개. 두 식으로부터 역행렬을 구할 수 있다.
여기서 가우스 조단 방법은 두 식을 한번에 계산해버리는 거다.
일반화하면 가우스 조단 방법은 nxn 역행렬을 구할 때 n개 식을 한번에 하는 것임.
가우스 조단 방법을 적용하면 [A I] 가 [I A^-1]로 변하고 따라서 A^-1를 구할 수 있다. 즉, A를 I로 만들어주면 I는 A^-1가 된다. 그런데 왜 I가 A의 역행렬이 될까?
E[A I] -> [I ??]
A에 E를 곱하여 I가 되었다. 따라서 E는 A의 역행렬이다. '??'는 E에 I를 곱한 값이고 E x I = E다. 따라서 '??'는 A의 역행렬.
여기서 앞에서 배웠던 블럭 곱하기가 사용된 걸 체크! [A I]는 A와 I로 파티션이 나누어져 있다.

Ax = b에서 x는 column이 하나임을 의미
AB에서 B는 column이 여러개 가지고 있음을 의미
Multiplication by columns
AB = A[b1 b2 b3] = [Ab1 Ab2 Ab3]. b1,b2,b3는 B의 columns.

A의 열의 갯수와 B의 행의 갯수가 같아야 곱하기가 가능

matrix multiplication을 보는 세가지 방법

1) AB의 i,j번째 값은 A의 i번째 row와 B의 j번째 column의 inner product.

2) 모든 AB의 column은 A의 columns의 combination.

3) AB의 각 row는 B의 rows의 combination.

Bonus
4) AB = Sum of (cols of A) x (rows of B)
B의 row을 A의 col의 각 요소로 곱한 값이 결과다.
 
associative: (AB)C = A(BC)
distributive : A(B + C) = AB + AC and (B+C)D = BD + CD
not commutative : usually FE ≠ EF